Completely metrizable space

In mathematics, a completely metrizable space (complete topological space or topologically complete space) is a topological space (X, T) for which there exists at least one metric d on X such that (X, d) is a complete metric space and d induces the topology T. This is equivalent to the condition that X is a G_δ in its Stone–Čech compactification βX.

The set 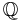of rational numbers is an example of a topological space that is metrizable but not completely metrizable.

See also

• Completely uniformizable space
• Metrizable space

References

• Willard, Stephen (2004). General Topology. Dover Publications. ISBN 0-486-43479-6.